Stručná a selektívna história čiernych dier vo fyzike
Čierne diery sú veľmi mysteriózne a fascinujúce objekty, ktorých existenciu prvýkrát reálne predpovedala až Einsteinova všeobecná teória relativity. Ako vysvetlím hneď v prvej časti, istá predstava o objekte, ktorý je tak hmotný, že ani svetlo mu nedokáže uniknúť, sa zrodila už pred všeobecnou relativitou, ale takáto klasická čierna diera má od tej einsteinovskej veľmi ďaleko, hoci základná vlastnosť ostáva: z čiernej diery nemôže uniknúť nič, ani svetlo, preto je čierna.
V Einsteinovej teórii sa však gravitácia neopisuje ako sila, ale ako zakrivenie geometrie priestoročasu. To so sebou prináša niektoré nečakané prvky. Ako uvidíme, čierne diery môžu rotovať a strhávať priestor okolo seba, môžu niesť elektrický náboj, možno z nich získavať energiu. Veľký prielom v skúmaní čiernych dier nastal, keď sa zistilo, že čierne diery majú termodynamické vlastnosti. Z Einsteinovej teórie plynú matematické teorémy o čiernych dierach, ktoré veľmi pripomínajú zákony tepla, tzv. termodynamické vety. Táto podobnosť našla šokujúce vyvrcholenie Hawkingovým objavom, že čierne diery v skutočnosti vyžarujú žiarenie, ako keby sa jednalo o teleso zahriate na určitú teplotu. Tento efekt Hawking objavil, keď sa pokúsil aplikovať zákony kvantovej mechaniky na čierne diery. Zavedenie kvantovej mechaniky však prináša ďalšie problémy v pochopení čiernych dier: je to problém spojený s informáciou. Podľa kvantovej mechaniky sa informácia nikdy nemôže stratiť, ale vyžarujúca čierna diera zdanlivo informáciu stráca. Keď do nej spadne napríklad počítač, ktorý zaiste obsahuje veľké množstvo informácií, tieto informácie sa pádom do čiernej diery stratia. Keď potom čierna diera vyžiari elektromagnetické vlnenie, rovnaké ako by vyžarovalo teleso určitej teploty, v tomto vlnení už daná informácia prítomná nie je. Hovorí sa tomu informačný paradox pre čierne diery.
Riešenie tohto paradoxu bolo predmetom tzv. "čiernodierovej vojny", ktorú viedli (v intelektuálnom zmysle) významní fyzici dneška: Stephen Hawking a Leonard Susskind. Hawking zastával názor, že informácia sa skutočne v čiernej diere stratí, Susskind naopak argumentoval, že tomu tak nie je. Vec sa skončila tak, že Hawking priznal porážku a začal zastávať Susskindov názor. Iní fyzici, napríklad Roger Penrose, však argumentujú, že Hawking sa vzdal príliš rýchlo. Penrose už dávno argumentuje, že zachovanie informácie v kvantovej mechanike sa naruší, keď do hry vstúpi gravitácia. Ja osobne považujem Penroseove argumenty za veľmi presvedčivé, ale pokúsim sa o objektívne zhodnotenie celej situácie. Výsledkom však je, že informačný paradox nie je dodnes uspokojivo a jednoznačne vyriešený.
Celá vec sa ešte viac zamotala celkom nedávno, keď známy strunový teoretik Polchinski prišiel s ešte šokujúcejším záverom, než bol Hawkingov objav žiarenia čiernych dier. Vysvetlenie tohto objavu, zatiaľ hypotetického, bude vyvrcholením celej série článkov o čiernych dierach, ale skúsim veľmi približne naznačiť, o čo ide. Jedným zo základov teórie relativity je Einsteinov princíp ekvivalencie. Ten hovorí, že pozorovateľ, ktorý voľne padá v gravitačnom poli, necíti gravitačné pole. Vieme, že ak stojíme vo výťahu, ktorý buď stojí, alebo sa rovnomerne pohybuje hore či dolu, cítime svoju tiaž: nohami tlačíme o podlahu. Ale keď sa výťah rozbieha smerom nahor, cítime sa o čosi ťažší, pretože naše telo sa svojou zotrvačnosťou bráni zrýchlenému pohybu výťahu. Naopak, ak sa výťah rozbieha smerom nadol, cítime sa o čosi ľahší, pretože telo sa zotrvačnosťou snaží zostať na mieste a teda nám podlaha "uteká pod nohami". Tí menej šťastní z nás majú aj extrémnu skúsenosť, kedy sa ocitli vo voľne padajúcom výťahu. Vtedy nám podlaha pod nohami uteká presne tak rýchlo, ako my spolu s výťahom padáme, takže vlastnú tiaž necítime vôbec. To je zmysel tvrdenia, že voľne padajúci pozorovateľ necíti vlastnú tiaž, nevníma gravitačné pole.
Čierna diera, pokiaľ ste ďaleko od nej, sa svojimi gravitačnými účinkami nijak nelíši od obyčajného telesa. Existuje však určitá vzdialenosť, tzv. horizont udalostí, za ktorou už žiaden objekt nemôže čiernu dieru opustiť. Ak ste nad horizontom udalostí, môžete na svojej osobnej rakete zapnúť motory, a ak sú dosť silné, môžete sa od čiernej diery vzdialiť. Ak ste pod horizontom, ani istoty vás nezachránia a žiaden motor nie je schopný vyvinúť silu, ktorá by vám umožnila čiernu dieru opustiť. Nutne vás čaká pád do stredu čiernej diery, do tzv. singularity.
Ale predstavte si, že sa o únik nesnažíte, len sa necháte voľne priťahovať čiernou dierou. Podľa princípu ekvivalencie necítite vlastnú tiaž, nevnímate gravitačné pole. Podľa klasickej Einsteinovej teórie, ak prekročíte horizont udalostí, nič si nevšimnete. Iná vec je, že v blízkosti čiernej diery pocítite tzv. slapové sily, ktoré vás budú deformovať, ak je raketa príliš veľká. Tieto sily vás v skutočnosti roztrhajú skôr, než dospejete k singularite. Ale fakt je, že na samotnom horizonte udalostí si nič zvláštne nevšimnete. Hovorí sa o "no drama" scenári, teda scenári, v ktorom sa na horizonte udalostí nič zvláštne nedeje, hoci spoza horizontu už niet návratu. Matematicky hovoríme, že horizont udalostí je len súradnicová singularita, kdežto stred čiernej diery je skutočná singularita priestoročasu. Tieto pojmy si v priebehu tejto série článkov vysvetlíme.
To, čo som doteraz popisoval, je štandardný priebeh pádu do čiernej diery tak, ako ho popisuje teória relativity. Keď však pridáme kvantovú mechaniku a snažíme sa pochopiť informačný paradox opisovaný vyššie, veci sa komplikujú. Hovorili sme o tom, že podľa kvantovej mechaniky sa informácia nemôže stratiť. Môže byť schovaná pod horizontom čiernej diery. Ale objav Hawkingovho žiarenia ukazuje, že čierne diery žiaria a postupne sa vyparujú, až nakoniec život čiernej diery skončí výbuchom, pri ktorom čierna diera zanikne. Ale to znamená, že zmizne aj horizont udalostí, takže informácia, ktorá bola skrytá pod ním, sa musí znovu vrátiť do sveta. Inými slovami, žiarenie, ktoré čierna diera behom svojho života vyžiarila, musí obsahovať práve toľko informácie, koľko do nej za celý život spadlo.
V kvantovej mechanike existuje mechanizmus, tzv. entanglement alebo previazanie častíc. Tento mechanizmus spočíva v tom, že dve častice, ktoré vznikli na jednom mieste, môžu byť navzájom previazané, aj keď sa postupom času dostanú ďaleko od seba. Zatiaľ nechajme bokom, čo presne to znamená. Ide o to, že ak sa informácia podľa kvantovej mechaniky nesmie stratiť, častice žiarenia, ktoré čierna diera vysiela, musia byť nejakým spôsobom previazané s časticami, ktoré do čiernej spadli. Susskindove a iných analýzy zase ukazujú, že častice, ktoré vychádzajú z čiernej diery, musia byť kvantovo previazané so všetkými časticami, ktoré čierna diera vyslala v minulosti. Podľa kvantovej mechaniky ale nemôže byť jedna častica súčasne previazaná s dvoma systémami: aj s časticou padajúcou dovnútra, aj s Hawkingovým žiarením. Jedno z možných riešení spočíva v tom, že previazanie padajúcej a vyletujúcej častice musí byť prerušené na horizonte udalostí. Toto prerušenie je doprevádzané uvoľnením veľkého množtva energie, ktoré je poeticky označované ako ohnivý prstenec - odtiaľ názov "firewall paradox".
Tento scenár však protirečí Einsteinovmu princípu ekvivalencie: pozorovateľ padajúci do čiernej diery bude pri prechode horizontom uškvarený ohnivým prstencom, zatiaľčo podľa pu ekvivalencie sa na horizonte nedeje nič zvláštne.
Popis, ktorý som podal, je veľmi nepresný a zjednodušený, ale cieľom týchto článkov je vysvetliť teóriu čiernych dier natoľko, aby som ho mohol spresniť a podrobnejšie vysvetliť. Tento problém je však nevyriešený a predstavuje jednu z najnovších hádaniek teoretickej fyziky.
Poďme sa teraz poklusom pozrieť na to, čo to čierne diery sú. Vysvetlím, čo je analógiou čiernych dier v klasickej fyzike, potom v ešte väčšom pokluse naznačím, ako sa na čierne diery pozerá Einsteinova teória relativity a nakoniec sa dotknem otázky reálnej existencie čiernych dier a toho, prečo v existenciu čiernych dier naozaj veríme. Podrobná analýza čiernych dier z hľadiska všeobecnej teórie relativity bude potom náplňou ďalších (a ďalších) článkov.
Čierna diera - klasický pohľad
Aj laickej verejnosti sú známe pojmy ako prvá a druhá kozmická rýchlosť. Predstavme si, že Zem je dokonalá guľa a zanedbajme odpor vzduchu. Keď kopneme do lopty, tá vyletí do nejakej výšky, ale potom spadne na zem a zastaví sa. Čím silnejšie do lopty kopneme, tým ďalej sa lopta samozrejme dostane. Môžeme si však predstaviť, že do lopty kopneme tak silno, že sa nevráti naspäť na zemský povrch, ale začne obiehať okolo Zeme po kružnici. Je to nereálne, pretože Zem nie je dokonalá guľa, takže našu loptu by i pri sebaväčšom športovom výkone zastavili hory, lesy, dobre vám je (P.O. Hviezdoslav). Ale ak by Zem bola dokonalá guľa, ak by lopta nebola spomaľovaná odporom vzduchu, môžeme predstaviť, že by sa lopta skutočne pohybovala okolo Zeme po kružnici. Rýchlosť, ktorú musíme lopte udeliť, aby sa tak skutočne pohybovala, sa nazýva prvá kozmická rýchlosť a pre planétu hmotnosti Zeme má hodnotu asi 8 km/s. Aby sme dokázali loptu takto nakopnúť, museli by sme denne robiť viac klikov, než pán premiér v hlavnom spravodajstve.
Skúsme teraz iný experiment: kopnúť loptu nahor. Zase platí, že gravitačné pole Zeme bude loptu brzdiť, takže táto sa časom vráti na zemský povrch. Ale zase si môžeme predstaviť, že loptu nakopneme tak silno, že opustí gravitačné pole Zeme a bude sa vzďaľovať do nekonečna. Potrebnej rýchlosti sa hovorí druhá kozmická rýchlosť a pre Zem má hodnotu asi 11 km/s.
Čím väčšia by bola hmotnosť planéty, tým väčšia bude aj druhá kozmická rýchlosť. Keby bola planéta dostatočne hmotná, druhá kozmická rýchlosť by sa rovnala rýchlosti svetla. Ak by bola planéta ešte hmotnejšia, ani svetlo by sa nemohlo dostať z gravitačného poľa planéty. Podobné úvahy viedli geológa Michella a matematika Laplacea v osemnástom storočí, kedy svetovej vede dominovala Newtonova klasická mechanika, k predstave o tak hmotnej hviezde, ktorá by neumožnila ani svetlu uniknúť z jej dosahu. Táto hviezda by bola pre vonkajší svet neviditeľná, ale mohli by sme ju registrovať na základe toho, že priťahuje všetko zo svojho okolia. Samotný názov čierna diera je dielom významného fyzika 20. storočia, pomerne nedávno zosnulého Johna Wheelera. Zaujímavosťou je, že spočiatku bol tento termín považovaný za vulgárny, pretože v očiach morálnych puristov evokoval niečo úplne iné než astrofyzikálny objekt.
Toto je klasický obraz toho, čo dnes nazývame čierna diera. Aby sme z povrchu čiernej diery mohli vyslať signál, musel by sa tento pohybovať nadsvetelnu rýchlosťou. Ale tento klasický pohľad na vec je veľmi zjednodušený a nevystihuje dnešnú predstavu o čiernej diere. Aby som ilustroval zásadný rozdiel medzi obama koncepciami, skúsim použiť nasledujúcu úvahu.
Keď sme zaviedli pojem druhej kozmickej rýchlosti, predpokladali sme, že nakopnutému objektu je udelená nejaká počiatočná rýchlosť. Táto rýchlosť sa zmenšuje vplyvom pôsobenia gravitačného poľa, ale ak je pôvodná rýchlosť dostatočná, nezmenší sa natoľko, aby objekt zostal uväznený v gravitačnom poli.
Ale predstavme si, že nejde o loptu, ale o raketu. Rakete nemusíme udeliť druhú kozmickú rýchlosť, aby opustila pole Zeme. Úplne stačí, ak motory budú pôsobiť rovnakou silou, ako gravitačné pole Zeme. Predstavme si raketu vznášajúcu sa napríklad meter nad zemou, ktorá má nulovú rýchlosť, ale jej motory sú tak silné, že vzdorujú gravitačnej sile a udržujú raketu v konštantnej výške meter nad zemou. Ak teraz do rakety len jemne pinkneme, bude sa pomaly, pomaličky dvíhať stále vyššie. Jej motory pôsobia stále rovnakou silou, takže raketa nespadne na zem, ale okrem toho sme jej udelili ešte slabý impulz smerom nahor, takže sa týmto smerom bude pohybovať. Čím ďalej bude raketa od zeme, tým slabšie bude gravitačné pole a teda motory budú rakete dokonca udeľovať nejaké zrýchlene, takže raketa sa bude od Zeme postupne vzďaľovať a to stále rýchlejšie. Takto unikne z gravitačného poľa Zeme.
Cieľom tohto príkladu je ukázať, že teleso, ktoré má uniknúť z poľa Zeme, v skutočnosti nemusí mať druhú kozmickú rýchlosť. Ak má vlastné a dostatočne silné motory a dostatok paliva, stačí ľubovoľne malá rýchlosť, aby sa to podarilo. Druhú kozmickú rýchlosť potrebuje len vtedy, ak vlastné motory nemá a musíme teda telesu hneď na začiatku udeliť tak veľkú rýchlosť, aby sa bez pohonu z gravitačného poľa Zeme vymanilo.
V teórii relativity je to inak.
Čierna diera - relativistický pohľad
Podrobný popis čiernej diery, ako nám ho dáva teória relativity, si odložíme do ďalších článkov. Teraz chcem len zdôrazniť, že relativistická čierna diera je niečo omnoho záhadnejšie než čierna diera podľa Michella či Laplacea. V klasickej mechanike neexistuje horná hranica pre rýchlosť. Fajn, rýchlosť svetla je asi 300 000 km/s, čo je extrémne veľká rýchlosť vzhľadom ku všetkým pozemským štandardom. Ale podľa klasickej mechaniky môže existovať ľubovoľne veľká rýchlosť, desať krát, stokrát, milión krát väčšia než rýchlosť svetla. V Newtonových časoch, keď vrcholom rýchlosti bol koňský povoz, sa nikto nemohol experimentálne presvedčiť, že rýchlosť nemožno zväčšovať neobmedzene.
Einsteinova špeciálna teória relativity však teoreticky ukázala, že rýchlosť svetla je medznou rýchlosťou pre všetky javy v prírode. Dnes túto skutočnosť vieme overiť aj experimentálne. V urýchľovačoch častíc sa urýchľujú elektróny, najľahšie dostupné častice, na rýchlosti blízke rýchlosti svetla, ale ani enormné zvyšovanie energie nedokáže tieto elektróny urýchliť až na rýchlosť svetla. Tým sa však nemyslí, že by naše mašiny neboli dosť výkonné, ide o niečo iné. Ak má elektrón malú rýchlosť, tak štvornásobné zväčšenie jeho energie povedie k dvojnásobnému zväčšeniu jeho rýchlosti. Ale pri vysokých rýchlostiach sa táto bilancia mení a môžeme dodávať energie koľko chceme, rýchlosť elektrónu sa bude zvyšovať stále pomalšie a pomalšie. Teória aj experiment ukazujú, že čím bližšie rýchlosti svetla sme, tým menší efekt má ďalšie zvyšovanie energie. Takže by sme museli elektrónu dodať nekonečne mnoho energie, aby dosiahol rýchlosť svetla. Celá vec je na dlhšiu debatu, ale môžeme brať ako teoreticky i experimentálne dokázaný fakt, že nič sa nemôže pohybovať rýchlejšie ako svetlo. Častice, ktoré majú hmotnosť, sa dokonca musia pohybova vždy rýchlosťou menšou. Jedine častice s nulovou hmotnosťou sa pohybujú vždy práve rýchlosťou svetla. Konkrétne svetlo je elektromagnetická vlna, ktorú sprostredkúvajú častice zvané fotóny. Tie sa vo vákuu vždy pohybujú rýchlosťou svetla a nikdy menšou ani väčšou.
Takže podľa klasickej teórie, svetlo síce nemôže z čiernej diery uniknúť, ale objekt s vyššou rýchlosťou by mohol. Podľa teórie relativity nemôže z čiernej diery uniknúť vôbec nič, pretože nič nemôže mať vyššiu rýchlosť než svetlo.
Stále však zostáva možnosť, že by z čiernej diery mohla uniknúť raketa s dostatočne silnými motormi. Tá síce nemôže dosiahnuť rýchlosť svetla, ale s dostatočne silnými motormi by takúto rýchlosť ani nepotrebovala. Stačilo by, aby dokázala vzdorovať gravitačnému poľu čiernej diery, a potom by jej stačila ľubovoľne malá rýchlosť. Všeobecná teória relativity však hovorí, že ani toto nie je možné. Prečo?
Odpoveď spočíva v tom, ako sa vo všeobecnej relativite popisuje gravitácia. Nie je to obyčajná sila, je to prejav geometrie priestoru, či skôr priestoročasu. Nasledujúca úvaha je síce veľmi zjednodušená a trochu skresľujúca, ale používa sa vo všetkej populárnej literatúre a teda ju použijem aj ja. Priestor bez gravitácie si môžeme predstaviť ako plochú rovinu:
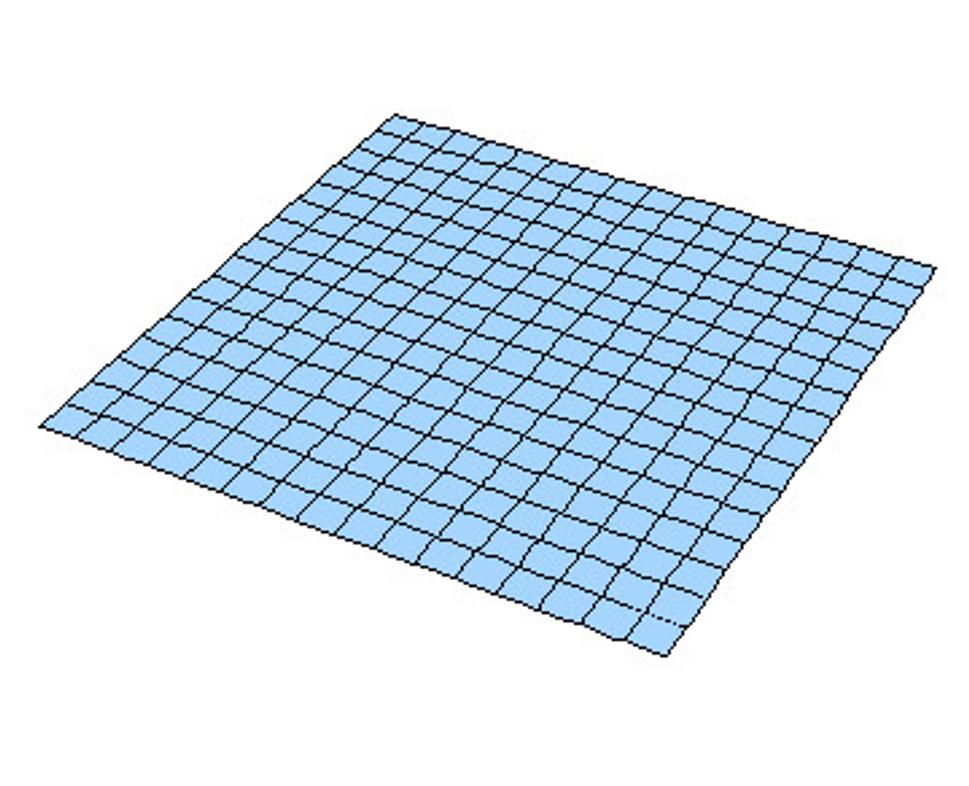
V tejto rovine je znázornená i sústava rovnobežných a kolmých priamok. Ak v priestore neexistujú telesá, ktoré sú zdrojom gravitácie, priamky sú rovné čiary. Pozorovateľ, ktorý sa bude pohybovať rovnomerne, bez zmeny svojej rýchlosti, sa bude pohybovať po priamke. Predstavme si ale, že rovinu trochu zdeformujeme:
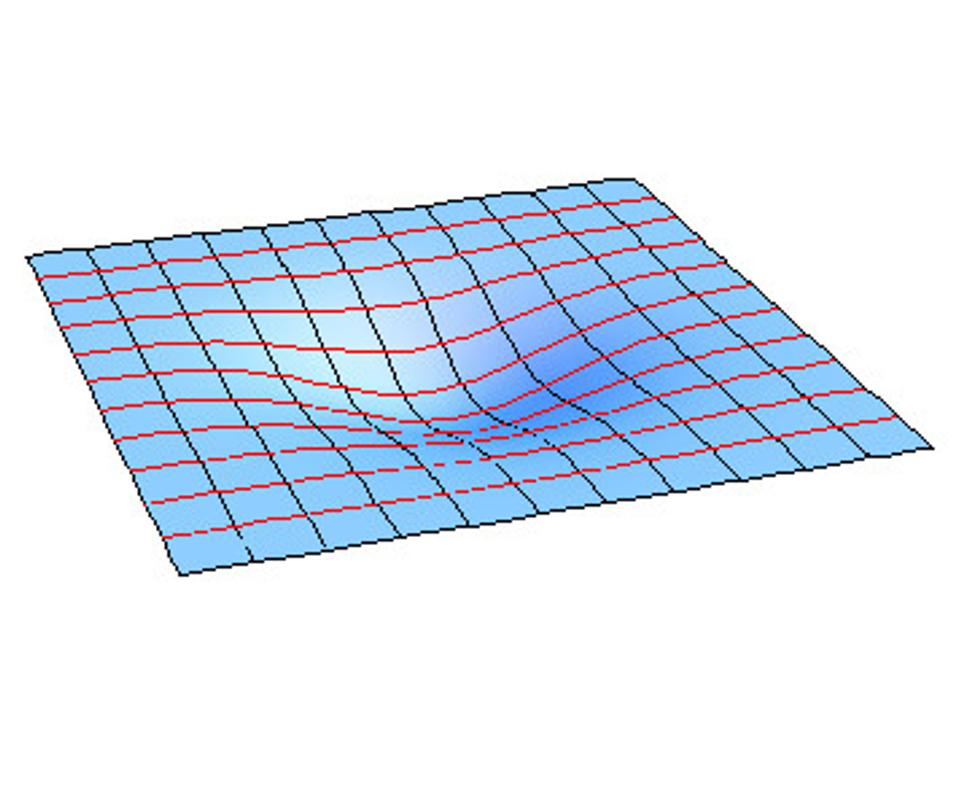
Na tejto zdeformovanej rovine už pôvodné priamky nie sú priamky, ale krivky. Všimnime si, že vo väčšej vzdialenosti od priehlbiny sú priamky skoro neznemené, sú zdeformované len veľmi málo. Ale všimnime si aj čiernu krivku (v pôvodnej rovine to bola priamka), ktorá prechádza cez priehlbinu. Začína ako priamka, ale vplyvom priehlbiny sa zakriví, pretože sleduje geometriu priehlbiny, takže to vyzerá, že sa vlastne priblížila ku dnu priehlbiny. Ak si predstavíme, že na našej deformovanej rovine žije nejaký dvojrozmerný chrobáčik, ktorý sa snaží pohybovať po priamke, tento chrobáčik to vyhodnotí tak, že ho "niečo" pritiahlo. Všetko, čo sa snaží pohybovať rovnomerne po priamke, sa v skutočnosti musí pohybovať po zakrivenej čiare, ktorá sleduje zakrivenie plochy.
Ale náš pomyselný dvojrozmerný chrobák nevníma, že jeho plocha je zakrivená do tretieho rozmeru, vidí len to, že ho niečo priťahuje. Túto tajomnú silu nazve gravitácia, presne tak ako my v trojrozmernom priestore. Podľa Einsteina je gravitácia v skutočnosti prejavom toho, že geometria nášho priestoru nie je geometriou plochého, ale zakriveného priestoru. Tam, kde sa nachádzajú telesá, sa priestor deformuje a my to vyhodnotíme tak, že nás tieto telesá priťahujú. Toto Einsteinovo vysvetlenie gravitácie prirodzene vysvetľuje dávno známy fakt, že v gravitačnom poli sa telesá pohybujú všetky úplne rovnako, nezávisle na ich hmotnosti. Vďaka tomu sa napríklad kozmonaut v rakete, ktorá obieha okolo Zeme, pohybuje rovnako ako raketa. Keby to tak nebolo, tlačil by na steny rakety, ale to sa nedeje: kozmonaut pociťuje beztiažový stav. Je to ďalší prejav princípu ekvivalencie, o ktorom bola reč vyššie.
Celé je to samozrejme zložitejšie a to minimálne v dvoch smeroch. Prvý je ten, že podľa teórie relativity sa nezakrivuje priamo priestor, ale priestoročas. O tomto pojme som už písal, pre názornú predstavu odporúčam svoj ostatný článok
http://scholtz.blog.sme.sk/c/341695/Binarne-systemy-vo-vseobecnej-teorii-relativity.html
Komplikácia spočíva v tom, že hoci sa teleso v trojrozmernom priestore môže pohybovať ľubovoľnou rýchlosťou menšou než rýchlosť svetla, v priestoročase sa teleso vždy pohybuje rýchlosťou svetla. V uvedenom článku som diskutoval aj pojem svetelného kužeľa, ktorý je pre pochopenie veci podstatný, ale vrátim sa k tomu v ďalších článkoch. V obrázkoch, ktoré som načrtol vyššie, však nie je vidno, akou rýchlosťou sa teleso pohybuje, kým v priestoročasovom diagrame je aj rýchlosť podstatná.
Druhá komplikácia spočíva v tom, že podľa teórie relativity je náš štvorrozmerný priestoročas síce zakrivený, ale nie do nejakého piateho rozmeru. V obrázkoch vyššie sme si vedeli predstaviť dvojrozmernú rovinu v trojrozmernom priestore, takže chápeme, že rovinu možno ohnúť do tretieho rozmeru. Ale štvorrozmerný priestoročas nie je ohnutý do piateho rozmeru. Jeho krivosť je vnútornou, intrinsickou vlastnosťou. Aj na povrchu Zeme sme schopní zistiť, že je zakrivený. Napríklad tak, že necháme na rovníku vyplávať dve lode smerom na sever. Po veľmi dlhý čas sa nám bude zdať, že lode plávajú rovnobežne vedľa seba, ale nakoniec sa ich dráhy pretnú v severnom póle. Skutočnosť, že sa rovnobežky pretnú, je typický prejav krivosti priestoru. V tomto prípade je to však zase tak, že povrch Zeme je ohnutý do tretieho rozmeru. Predstaviť si priestor s neeuklidovskou geometriou si nedokážeme a musíme veriť len matematickým rovniciam a experimentom.
Takže navzdory všetkým výhradám týkajúcim sa obmedzenosti našej predstavivosti, toto je obsah teórie relativity: gravitácie nie je skutočná sila, je to prejav toho, že geometria priestoru je zakrivená.
Teraz sa vráťme k čiernym dieram. Existuje krásny a exaktný matematický spôsob, ako znázorniť vlastnosti čiernych dier v tzv. Penroseovom diagrame a bude mi cťou čitateľov s týmto spôsobom oboznámiť. Dnes sa však obmedzím zase len na veľmi schematický náčrt. Ak bude zakrivenie priehlbiny príliš veľké, bude to vyzerať nejak takto:
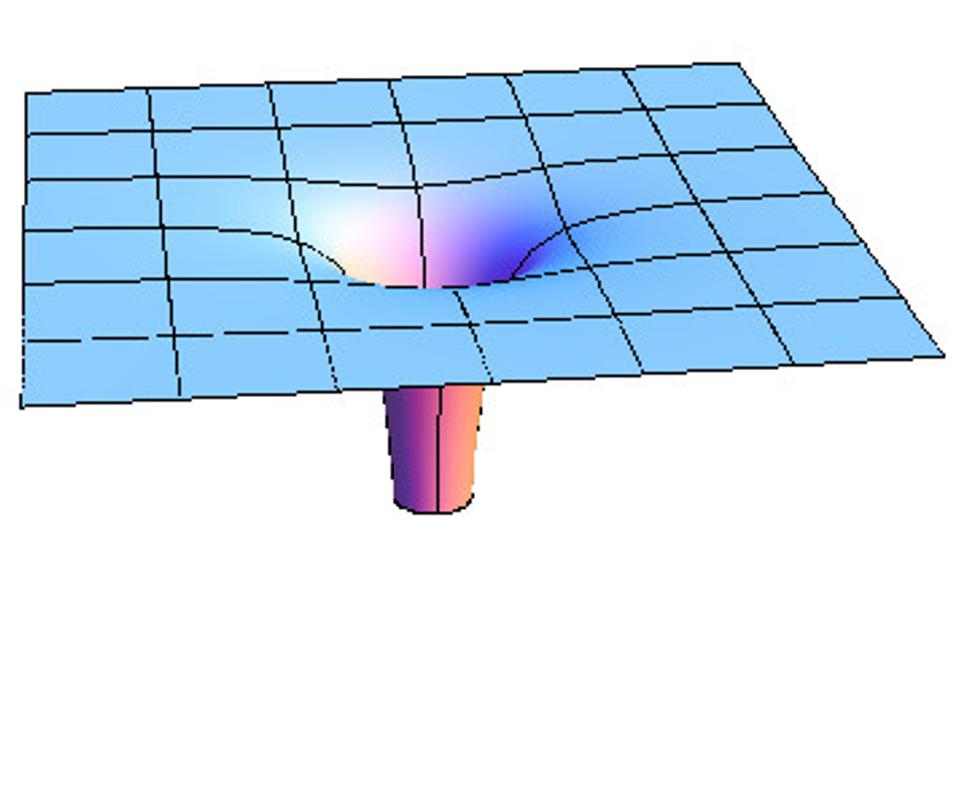
V tomto obrázku je celkom zjavné, kde priehlbina začína. Celá plocha je všade skoro rovná (rozprestiera sa od nekonečna do nekonečna, ale nakreslil som len kúsok), a ďaleko od priehlbiny vyzerajú priamky ako priamky. Ale niektoré priamky, ktoré sa dostanú cez okraj priehlbiny, do nej spadnú a už sa nedostanú von. Okraj priehlbiny, to je horizont udalostí, tak ako sme ho opísali vyššie. Stred priehlbiny je singularita, miesto, kde je krivosť priestoru nekonečne veľká. Striktne vzaté, samotný stred priehlbiny už do priestoru nepatrí.
V klasickom prípade vyššie sme hovorili, že raketa v skutočnosti nemusí mať druhú kozmickú rýchlosť, aby opustila gravitačné pole Zeme, stačia dosť silné motory a ľubovoľne malá rýchlosť. Ale v relativistickej teórii je to inak. Pád do singularity nie je daný tým, že nevieme vyrobiť dostatočne silné motory, ale tým, že po prekročení horizontu udalostí (okraja priehlbiny) musí raketa nutne sledovať zakrivenie priestoru. V klasickej teórii relativity nie je možné z čiernej diery uniknúť vôbec žiadnym spôsobom. Z čiernej diery nemôže uniknúť svetlo, ani žiaden hmotný objekt, ba dokonca ani prepis rozhovoru Š.H. s B.S.
Ako čierne diery vznikajú?
Čierna diera, ako sme ju práve popísali, je riešením Einsteinových rovníc gravitačného poľa a historicky to bolo dokonca prvé objavené riešenie týchto rovníc. Autorom riešenia je Karl Schwarzschild, čo bol paradoxne meteorológ, ale aj zdatný matematik. Svoje riešenie objavil veľmi krátko potom, čo Einstein teóriu relativity publikoval. Sám Einstein si uvedomoval, že jeho rovnice sú veľmi zložité a spočiatku váhal, či ich vôbec bude možné pre nejaký fyzikálne zaujímavý prípad vyriešiť. Dnes už však poznáme veľké množstvo presných riešení Einsteinových rovníc a záujemcom môžem poskytnúť odkazy na literatúru.
Schwarzschild si riešenie zjednodušil tým, že predpokladal sférickú symetriu riešenia. Sférická znamená guľová. Inými slovami, uvažoval zdroj gravitačného poľa taký, že jeho gravitačné pole závisí len od vzdialenosti, ale nie od smeru. V istom priblížení je aj pole Zeme sféricky symetrické: gravitačná sila od Zeme vo vzdialenosti milión kilometrov od Zeme je rovnaká nezávisle na tom, či je to milión kilometrov smerom na sever, milión kilometrov nad rovníkom alebo akýmkoľvek iným smerom. Ak učiníme tento predpoklad o sférickej symetrii, Einsteinove rovnice sa veľmi zjednodušia a dnes ich vie vyriešiť každý študent teórie relativity.
Schwarschildovo riešenie teda popisuje sféricky symetrickú čiernu dieru. Jeho výsledok bol neskôr doplnený o tzv. Birkhoffovu teorému, ktorá zhruba hovorí, že jediné sféricky symetrické riešenie Einsteinových rovníc je to Schwarzshildovo. Vďaka tejto teoréme bolo možné ukázať (Chandrasekhar, Oppenheimer), že dostatočne hmotná guľová hviezda nutne skončí ako čierna diera. Čo znamená "dostatočne hmotná"? Oppenheimer, Volkoff a Tolman ukázali, že ak hmotnosť hviezdy prekročí 3 až 4 násobok hmotnosti Slnka, a nepodarí sa jej včas odvrhnúť svoj materiál (napríklad výbuchom supernovy), gravitačné pole bude tak silné, že stlačí celú hmotu hviezdy pod kritický polomer a z hviezdy sa stane čierna diera. Hovoríme tomu gravitačný kolaps (navrhujem tiež neologizmus gravitačná viróza).
Vo vesmíre poznáme mnoho objektov, ktoré túto hranicu prekračujú a mnohé z nich by teda mali skončiť ako čierna diera.
Podstatným predpokladom v prácach TOV (Tolman,Oppenheimer,Volkoff) bola ona sférická symetria. Ak je hviezda presne guľová a hmotnejšia než TOV hranica, hviezda sa premení na čiernu dieru. Ale čo keby nebola presne guľová? Bude tento výsledok stále platiť? Stane sa reálna hviezda, ktorá nie je presne guľová, čiernou dierou?
Táto otázka nie je triviálna, ako by sa mohlo zdať. Aj v newtonovskej teórii totiž môže vzniknúť singularita, ak na začiatku predpokladáme, že kolabujúca hviezda má presne guľový tvar. Ale ak bude ten tvar čo len trochu iný, kolabujúce častice sa minú a žiadna singularita nevznikne. Takže v princípe by aj vznik Schwarzschildovej čiernej diery mohol byť len dôsledkom príliš zjednodušujúceho predpokladu o sférickej symetrii. Fyzici v tom čase ešte veľmi neverili existencii čiernych dier a preto sa im zdalo, že ak hviezda nebude presne guľová, singularita nevznikne. Aj sám Einstein si to myslel. A pretože žiadna reálna hviezda nemôže byť presne guľová, vyvodili z toho, že Schwarzschildovo riešenie je síce pekný, ale úplne nefyzikálny výsledok.
Takéto otázky sa často riešia analýzou stability riešenia a pomocou poruchového počtu. O čo ide? Einsteinove rovnice pre hviezdu všeobecného tvaru riešiť nevieme, ale pre presnú guľovú hviezdu máme Schwarzschildovo riešenie. Preto môžeme uvažovať sféricky symetrickú hviezdu a potom uvažovať maličkú poruchu sférickej symetrie. Napríklad, že hviezda nie je presná guľa, ale elipsoid, ktorý sa na guľu veľmi podobá. Touto cestou sa vydala svetovo uznávaná ruská skupina pod vedením Zeľdoviča a Novikova. Pomocou zdĺhavých, komplikovaných a neprehľadných výpočtov ukázali, že ak opustíme predpoklad o sférickej symetrii, čierna diera nevznikne. V tom čase boli títo Rusi asi jediní ľudia na svete, ktorí dokázali tak komplikované výpočty doviesť do konca.
Ale medzitým sa mladý začínajuci a talentovaný matematický fyzik Roger Penrose vydal úplne inou cestou. Nesnažil sa riešiť zložité sústavy nelineárnych rovníc, no snažil sa pochopiť celú problematiku z iného hľadiska. Je treba povedať, že vtedy ešte fyzika nebola tak matematická ako dnes. Fyzici chápali matematiku len ako nástroj na riešenie fyzikálnych problémov. Fyzik tej doby rozumel tomu, že daný jav je popísaný nejakými rovnicami a tieto rovnice sa snažil riešiť. A keď to boli komplikované rovnice, bolo ich treba riešiť s ešte väčšou vervou.
Penrose mal naproti tomu skôr matematické zázemie a ovládal mnohé oblasti matematiky. Uvedomil si, že na celý problém sa dá dívať jednoduchšie v pojmoch tzv. diferenciálnej topológie. Miesto toho, aby uvažoval o kolapse reálnej fyzikálnej hviezdy, čo zahrnuje množstvo komplikovaných detailov, položil si všeobecnejšiu otázku, po akých krivkách sa môžu pohybovať častice v zakrivených priestoročasoch. A ukázal, že ak sa tieto krivky v nejakom čase zbiehajú do jednej oblasti (nie nutne bodu), tak v neskoršom čase nutne vytvoria singularitu. Budeme o tom hovoriť neskôr v ďalších článkoch.
Podstatné je, že Penrose sa neopieral o nejaké detaily týkajúce sa reálnych astrofyzikálnych objektov, ukázal úplne všeobecne, bez dodatočných predpokladov, len z Einsteinových rovníc, že kolabujúci systém musí vytvoriť singularitu. Keď prezentoval svoje výsledky, fyzici mali tendenciu mu neveriť, pretože jeho argumentom nerozumeli a Zeľdovičova skupina pracovala osvedčenými metódami. Neskôr však Rusi našli vo svojich výpočtoch chyby, fyzici sa medzitým zorientovali v diferenciálnej topológii a tak definitívny záver znel, že Penrose má pravdu.
To je veľmi dôležitý výsledok. Hovorí, že dostatočne hmotná hviezda, ktorá neodvrhne svoj materiál včas, naozaj skončí ako čierna diera. Neexistuje spôsob, ako tomu zabrániť. Kolapsu hviezdy inak bránia mnohé aspekty, napríklad vnútorný tepelný tlak, kvantovomechanické javy, vylučovací princíp. Ale ak hviezda prekročí určitú hmotnosť, nie je cesty späť, kolaps je nevyhnutný.
Avšak z toho plynie, že množstvo objektov, ktoré v okolitom vesmíre vidíme, bude musieť skončiť ako čierna diera a množstvo iných objektov už tak dávno skončilo. Takže z hľadiska dnešnej fyziky nemožno reálne pochybovať o existencii čiernych dier.
Iná vec je, že čiernu dieru nemôžeme priamo vidieť a teda sa priamo presvedčiť o jej existencii. Ich prejavy však vidíme nepriamo. Napríklad v dvojhviezdnych systémoch, kde je jednou zložkou hviezda a druhou čierna diera. Vtedy môže dôjsť k tomu, že materiál z hviezdy je priťahovaný čiernou dierou a vidíme tak oblaky plynu, ktoré vychádzajú z hviezdy a potom sa strácajú v temnote. Problém je, že to, čo spôsobuje presun hmoty, môže byť aj neutrónová hviezda, tie totiž majú tiež veľmi silné gravitačné polia. Z pohybu hviezdy, ktorá materiál stráca, však vieme určiť, akú hmotnosť musí mať jej družka. Ak je nad kritickou hranicou, musí to byť čierna diera, a takých systémov poznáme veĺa. Sú tiež veľmi dobré dôvody veriť, že v centre každej galaxie, i v tej našej, sa nachádza supermasívna čierna diera. Takže aj keď čiernu dieru nemôžeme priamo vidieť, o ich existencii dnes existujú veľmi presvedčivé dôkazy.
Čo ďalej?
Čierne diery sú fascinujúce tým, že na ich popis je treba zložitú matematiku, ale pritom sú to najjednoduchšie objekty aké poznáme. Je to preto, že aby ste popísali čiernu dieru, stačí vám poznať tri jej vlastnosti: hmotnosť, rýchlosť rotácie a elektrický náboj. Skúste si predstaviť, že by ste pomocou troch čísel popísali ľudský mozog. Nemožné.
A predsa sú čierne diery tajomné. Sú to objekty, v ktorých sa prejavujú extrémne stránky prírody: singularity, horizont udalostí, strata informácie, možno ohnivé prstence predpovedané firewall paradoxom. Naše teórie výborne fungujú v bežných podmienkach a to tak dobre, že dnes nepoznáme žiaden konkrétny proces, ktorý by odporoval našim teóriám. Niektoré javy sú síce tak zložité, že naše teórie nevieme aplikovať, ale to je iná otázka.
Dnešná teoretická fyzika je výrazne v predstihu pred experimentálnou. Naše teórie siahajú ďaleko za rámec toho, čo sú dnešní experimentátori schopní preveriť. V tejto situácii je pre pokrok teórie dôležité analyzovať známe veci z nových rôznych uhlov, snažiť sa do dôsledkov pochopiť implikácie súčasných teórií. Čierne diery sú vynikajúcim laboratóriom pre tieto myšlienkové experimenty. Na začiatku sa fyzici snažili zdôvodniť, prečo čierne diery nemôžu existovať, potom prijali ich nevyhnutnosť, pochopili mnohé ich vlastnosti. Keď už si mysleli, že im rozumejú, objavil Hawking, že čierny diery vyžarujú, čo sa zdá byť proti samotnej podstate čiernych dier. A keď už sa zmierili s tým, že čierne diery skutočne vyžarujú, prišiel firewall paradox, v ktorom proti sebe stoja základné fyzikálne princípy. Preto je to fascinujúca oblasť ľudského snaženia a usilovania.
Ako som predznačil v úvode, mojim cieľom je prejsť spolu s čitateľmi všetkými podstatnými vlastnosťami čiernych dier. Na konci tejto cesty pochopíme, prečo je firewall paradox tak veľkou výzvou pre súčasnú fyziku.






