Čierne diery, časť III

Priestoročasový interval

V závere minulého článku sme zaviedli pojem priestoročasového intervalu. Stručne zopakujem a trochu preformulujem ústrednú myšlienku. Minkowského priestoročas je abstraktný matematický priestor, ktorý vznikne, ak ku trom priestorovým osám x, y, z pridáme ešte jednu časovú. To si samozrejme nevieme predstaviť, pretože priestoročas je štvorrozmerný, kdežto my sme obmedzení trojrozmernou predstavivosťou. Preto v priestoročasových diagramoch zakresľujeme len jednu alebo dve priestorové osi a jednu časovú.

Priestoročas je množina udalostí. Zdôrazňujem, že ak hovoríme o udalostiach, abstrahujeme od toho, čo sa stalo a zaujíma nás len kedy a kde sa to stalo. Slovami Minkowského, udalosť je niečo, čo sa stalo v určitom čase na určitom mieste. Každý pozorovateľ preto bude popisovať udalosť štvoricou súradníc t, x, y, z, kde t je čas, v ktorom sa udalosť odohrala, a x, y, z sú obvyklé priestorové súradnice.

Minule som veľkú pozornosť venoval vysvetleniu, že takto definovaný priestoročas môže byť užitočnou pomôckou na to, aby sme znázorňovali pohyb telies v čase v diagrame, ale sám o sebe neprináša žiadny nový poznatok ani hlbší vhľad do popisu reality. To, čo robí priestoročas revolučným pojmom, je tzv. metrika (tento pojem som minule oficiálne nezaviedol). Uvažujme dve udalosti U₁ a U₂. V súlade s tým, čo sme si povedali, tieto udalosti sú plne charakterizované svojimi súradnicami. Môžeme to zapísať symbolicky takto:

.

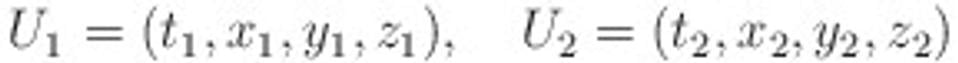
Pred teóriou relativity mali zmysel tieto dve otázky: aká je priestorová vzdialenosť týchto dvoch udalostí? A aký čas uplynul medzi týmito dvoma udalosťami? Podľa Pythagorovej vety (pre tých, ktorí nevedia, kto bol Pythagoras len pripomeniem, že to bol manžel starej Pythagorovej) je priestorová vzdialenosť daná vzťahom

,

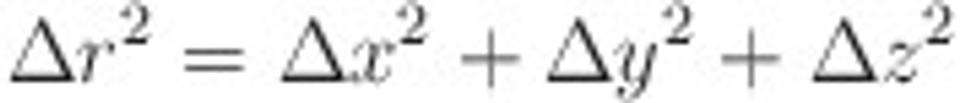
kde grécke písmeno &\delta; (veľká delta) znamená rozdiel x-ových, y-ových a z-ových súradníc, teda

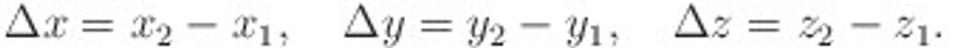
Priestory, v ktorých sa vzdialenosť počíta podľa hore uvedeného vzťahu pre Δr sa nazývajú euklidovské.

Časový interval, ktorý medzi oboma udalosťami uplynul, je zase daný vzťahom

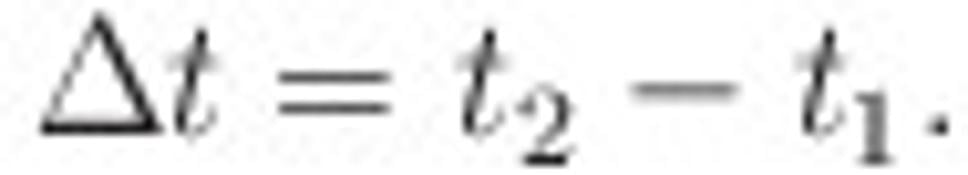
Do tejto základoškolskej matematiky vniesla teória relativity určité zmeny. V špeciálnej teórii relativity vzdialenosti a čas závisia na pozorovateľovi. Ak sledujeme pohybujúce sa hodiny, uvidíme ich tikať pomalšie, než keby stáli. Ak sledujeme pohybujúcu sa tyč, uvidíme ju skrátenú v smere pohybu. Preto súradnice udalostí v skutočnosti závisia od pozorovateľa, ktorý tieto udalosti sleduje. To je zásadný prínos teórie relativity: priestor a čas sú relatívne, závisia od pozorovateľa. To znamená, že iný pozorovateľ by na vyššie spomenuté dve otázky odpovedal inak, než my. Pre neho by udalosti U₁ a U₂ mali iné súradnice a preto by dospel aj k inej priestorovej vzdialenosti, aj inému časovému intervalu, ktorý medzi udalosťami uplynul.

Einstein publikoval špeciálnu teóriu relativity v roku 1905. O tri roky na to, myslím, že to bolo v roku 1908, si matematik Herman Minkowski uvedomil, že priestorové a časové vzdialenostisú síce rôzne, ale istá špeciálna kombinácia nie. Veličina, o ktorej hovoríme, sa nazýva priestoročasový interval a definujeme ju vzťahom

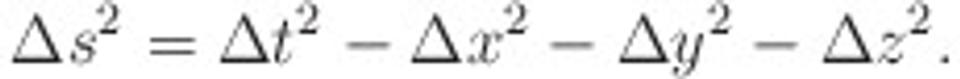
Upozorňujem, že používame jednotky, v ktorých sa rýchlosť svetla rovná 1, c = 1. V minulom článku som vysvetlil, prečo je to užitočné, takže sa nebudem opakovať. Len si musíme uvedomiť, že podľa tejto dohody majú čas a vzdialenosť rovnaké jednotky. Napríklad, ak povieme, že časový úsek má dĺžku 1, znamená to čas, ktorý svetlo potrebuje, aby prešlo vzdialenosť jeden meter. Tento čas je v štandardných jednotkách veľmi krátky (asi 3 miliardtiny sekundy), preto sú v teórii relativity tieto jednotky nepraktické. Dôvod, prečo to zdôrazňujem, spočíva v tom, že by niekoho mohlo zmiasť, že vo výraze pre Δs sčítavame čas a dĺžku. Ale je to OK, pretože obe súradnice meriame v rovnakých jednotkách, metroch.

Ale späť k jadru pudlíka. Ešte raz: Minkowski ukázal (vychádzajúc z teórie relativity), že hoci sú veličiny Δt, Δx, Δy, Δz pre každého pozorovateľa iné, veličina Δs z nich zostavená je rovnaká pre každého pozorovateľa. Keď si všimneme vzťah pre priestoročasový interval Δs, vidíme, že sa podobá na Pythagorovu vetu (porovnajte to s výrazom pre Δr!), ale znamienka sú tam inak: časový interval doň vstupuje s opačným znamienkom, než priestorové súradnice. Ale vzhľadom na podobnosť výrazov pre Δr a Δs je prirodzené aj Δs interpretovať ako vzdialenosť. Nie je to však priestorová vzdialenosť, ani časová vzdialenosť, je to vzdialenosť dvoch udalostí v abstraktnom štvorrozmernom priestoročase. Táto vzdialenosť nezávisí od pozorovateľa, hovoríme, že je to invariant (invariant = veličina, ktorá je pre všetkých rovnaká).

Priestoročasový interval má aj fyzikálny význam: je to vlastný čas pozorovateľa pohybujúceho sa po určitej svetočiare, ale s tým sa detailnejšie oboznámime v ďalších článkoch.

V matematike sa priestory, v ktorých je možné určovať vzdialenosti medzi jednotlivými bodmi, sa nazývajú metrické priestory. Výraz pre Δs teda definuje spôsob, ako určovať vzdialenosti medzi bodmi priestoročasu (udalosťami) a preto robí z Minkowského priestoročasu metrický priestor. Spôsob, ktorým tieto vzdialenosti určujeme sa potom označuje slovom metrika. Takže v klasickom trojrozmernom priestore je metrika daná vzťahom

,

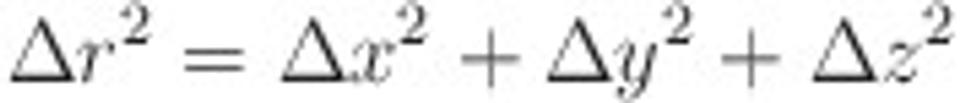
kým v Minkowského priestoročase je metrika daná vzťahom

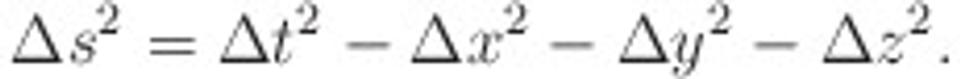
Podobnosť je zjavná, rozdiely tiež. Poďme preskúmať práve to, v čom sa tieto metriky líšia. To úzko súvisí s kauzalitou v teórii relativity.

Kauzálna štruktúra priestoročasu

Najprv sa pozrime na nasledujúci obrázok, hneď vysvetlím, čo na ňom vidíme.

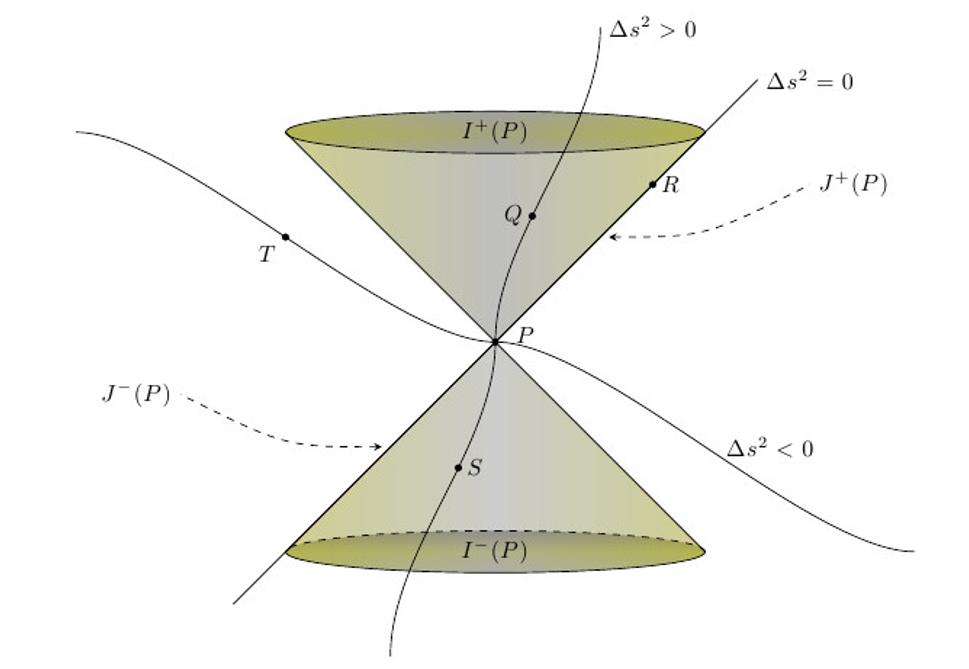
Takže...na obrázku vidíme priestoročasový diagram. Čas v ňom plynie smerom nahor. Všimnime si bod P, teda nejakú ľubovoľne zvolenú udalosť priestoročasu. Predpokladajme, že v tejto udalosti bol vyslaný svetelný signál všetkými smermi do priestoru. Vytieňovaná oblasť nad bodom P predstavuje množinu udalostí, kam svetlo dospeje v neskorších časoch. V minulom článku som vysvetlil, že ak prijmeme dohodu, že rýchlosť svetla je c = 1, svetlo sa v priestoročasovom diagrame šíri pod uhlom 45 stupňov. Na obrázku som vyznačil bod R. Ak z udalosti P vyšleme svetelný signál, bod R je jeden z bodov, kam svetlo v neskoršom čase dorazí. Priestoročasový interval Δs medzi udalosťami P a R je nulový. Všetky udalosti, pre ktoré platí Δs = 0, tvoria hranicu tzv. svetelného kužeľa. Pretože nič sa nemôže pohybovať rýchlejšie než svetlo, udalosť P nemôže mať nijaký vplyv na udalosti, ktoré ležia mimo svetalný kužeľ. Napríklad bod T na obrázku reprezentuje takú udalosť, ktorá leží mimo svetelného kužeľa. Priestoročasový interval medzi udalosťami P a T je záporný. Naopak, svetočiara každej častice, ktorá sa pohybuje rýchlosťou menšou než je rýchlosť svetla leží vnútri svetelného kužeľa. Na obrázku ju reprezentuje udalosť Q. Tá leží vnútri kužeľa a priestoročasový interval medzi bodmi P a Q je kladný.

Všimnime si, že zatiaľ čo vzdialenosť v euklidovskom priestore (spomenieme si na výraz pre Δr) je vždy kladná (nanajvýš nulová), v priestoročase môže byť kladná, nulová aj záporná. V euklidovskom priestore je vzdialenosť nulová len vtedy, keď sa jedná o vzdialenosť dvoch totožných bodov. V priestoročase je nulová vzdialenosť všetkých udalostí, ktoré sú spojené svetelným signálom. Preto o metrike priestoročasu hovoríme, že je pseudoeuklidovská, nie euklidovská.

Vzdialenosti v priestoročase možno teda klasifikovať do troch tried:

- časupodobné; to sú tie, pre ktoré Δs² > 0, ako pre udalosti P a Q na obrázku. Medzi takýmito udalosťami môže existovať príčinná súvislosť, pretože spolu môžu komunikovať, častica sa môže dostať z P do Q podsvetelnou rýchlosťou.

- svetlupodobné; to sú tie, pre ktoré Δs² = 0, ako pre udalosti P a R na obrázku. Takéto udalosti môžu byť spojené svetelným signálom, teda spolu môžu komunikovať, ale žiadna častica, ktorá sa pohybuje pomalšie než svetlo, sa z P do R dostať nemôže.

- priestorupodobné; pre ne platí Δs² < 0, ako pre udalosti P a T na obrázku. Tieto udalosti nemôžu spolu komunikovať, svetlo sa nemôže dostať z jednej do druhej (a teda ani nič iné).

(Poznámka. Ak vás trápi, ako môže byť druhá mocnina Δs² záporná, berte to tak, že Δs² je len skratka pre výraz, ktorým je táto veličina definovaná. Môžete to brať aj tak, že samotné Δs je v takom prípade komplexné, ale túto úvahu nebudeme potrebovať. Matematicky je Δs² tzv. kvadratická forma, a tá môže mať aj záporné hodnoty.)

Uvažujme ešte raz svetelný kužeľ bodu P na obrázku hore. Čas plynie smerom nahor a doteraz sme uvažovali len budúcnosť bodu P. Horná časť kužeľa sa nazýva budúci svetelný kužeľ. Všetky udalosti, ktoré ho tvoria, patria do budúcnosti bodu P. Táto množina sa tiež nazýva kauzálna budúcnosť bodu P a značí sa J⁺(P). Je to množina všetkých udalostí, ktoré je možné s bodom P spojiť časupodobnou alebo svetlupodobnou krivkou. Vnútro budúceho svetelného kužeľa (tým myslím svetelný kužeľ bez plášťa) je zase tvorené len tými udalosťami, ktoré je možné z bodu P dosiahnuť časupodobnou krivkou. Táto množina sa nazýva chronologická budúcnosť bodu P a značí sa I⁺(P).

Kauzálna budúcnosť bodu P je teda tvorená všetkými udalosťami Q, na ktoré môže mať udalosť v bode P aspoň v princípe vplyv. Medzi udalosťami vnútri svetelného kužeľa môže byť vzťah príčiny a následku. Ak by napríklad udalosť P bolo uverejnenie článku v novinách a udalosť Q by bolo zatknutie extrémistov, medzi týmito udalosťami by v princípe (ale len v princípe) mohla existovať kauzálna súvislosť. V žiadnej vzťažnej sústave by sa udalosť Q nemohla javiť ako skoršia než P. Tým by sa porušila kauzalita. Minkowského geometria zabezpečuje, že toto sa nemôže stať. Ak bod Q leží v kauzálnej budúcnosti bodu P, potom každý pozorovateľ uvidí, že k udalosti Q došlo neskôr, než k udalosti P.

Spomeňme si na bod T z vyššie uvedeného obrázka. Ten je nakreslený "vyššie", než bod P a mal by teda zodpovedať udalosti, ktorá sa odohrala v neskoršom čase než udalosť P. Ale bod T nepatrí do kauzálnej budúcnosti bodu P, takže udalosť v P nemôže mať v princípe žiaden vplyv na udalosť T. Medzi týmito udalosťami žiadny vzťah príčina-následok nemôže existovať. Preto to, čo sa udalosť T odohrala neskôr než P, je skutočnosť závislá od pozorovateľa. Pre niektorého pozorovateľa sa bude javiť T v čase neskoršom, pre iného môžu byť udalosti T a P súčasné, pre ďalšieho nastane udalosť T skôr než P. Pretože tieto udalosti spolu nijak nesúvisia, vzťah príčiny a následku sa nemôže porušiť.

Podobné úvahy sa vzťahujú na minulý svetelný kužeľ, teda na obrázku jeho dolnú polovicu. Kauzálna minulosť J^-(P) je množina všetkých udalostí, ktoré mohli mať vplyv na udalosť P. Teda je to množina všetkých udalostí, z ktorých svetelný signál stihol doraziť do P.

Schwarzschildova čierna diera

Tak sme sa oboznámili so základmi Minkowského geometrie a s kauzálnou štruktúrou Minkowského priestoru. Tieto poznatky budeme v ďalších článkoch postupne prehlbovať, pretože pre pochopenie klasických aj kvantových vlastností čiernych dier to bude dôležité. Ale s tým, čo už vieme, môžeme pochopiť aspoň v hrubých rysoch niektoré zvláštnosti geometrie v okolí čier.

Doteraz sme sa zaoberali špeciálnou teóriou relativity, ale teraz smelo vyrazíme do teórie všeobecnej. Množstvo argumentov zatiaľ vynechám. Všeobecná teória relativity vysvetľuje gravitačné pole ako prejav toho, že priestoročas je zakrivený. Minkowského priestor, ktorý sme vyššie zaviedli, je síce pseudoeuklidovský, takže v ňom existujú vektory s nulovou dĺžkou, ale stále je to priestor plochý. Každé dva body sa dajú spojiť priamkou. Keď sa však v priestore vyskytujú hmotné objekty alebo polia, geometria sa zakriví podľa Einsteinových rovníc. S nimi vás tiež časom zoznámim.

Einsteinove rovnice sú veľmi komplikovanou sústavou nelineárnych parciálnych diferenciálnych rovníc. Keď ich Einstein po dlhých útrapách trvajúcich 10 rokov konečne našiel, sám neveril, že by sa mohlo nájsť nejaké presné riešenie týchto rovníc, ktoré by malo reálny fyzikálny význam. Krátko nato však meteorológ Karl Schwarzschild jedno presné riešenie našiel. Toto riešenie popisuje gravitačné pole okolo presne guľového objektu, ale obsahuje aj pár podivností. Čiastočne som o tom písal už v prvom článku. Časom sa ukázalo, že tieto podivnosti sú reálne a Schwarzschildovo riešenie vlastne popisuje pole okolo čiernej diery. Trvalo dosť dlho, kým sa vyjasnilo, že tietojekty podľa teórie relativity skutočne musia existovať.

Dnes už poznáme veľké množstvo presných riešení Einsteinových rovníc, ale stále platí, že len málo z nich má fyzikálny význam. Ak chceme Einsteinove rovnice vyriešiť, väčšinou musíme urobiť veľa zjednodušujúcich predpokladov, čo však znižuje hodnotu získaného riešenia. Paradoxne Schwarzschildovo riešenie patrí dodnes medzi najvýznamnejšie a najužitočnejšie riešenia Einsteinových rovníc.Ukazuje sa totiž, že pri kolapse dostatočne hmotného objektu, ktorý nerotuje, je Schwarzschildova geometria vlastne jediná možnosť. O mnoho rokov neskôr bolo nájdené aj riešenie pre rotujúcu čiernu dieru, jeho autorom je novozélanďan Roy Kerr. A zase platí, že kolapsom rotujúceho objektu nutne vznikne Kerrova čierna diera. Okrem presných riešení popisujúcich čierne diery má veľký význam ešte Friedmannovo-Walkerovo-Robertsonove-Lemaitrovo riešenie, ktoré popisuje vývoj vesmíru. Ostatné riešenia už tak zaujímavé nie sú.

Ako vieme, čierna diera je objekt s tak silnou gravitáciou, že ani svetlo z nej nemôže uniknúť. Tento fakt je dôsledkom geometrie priestoročasu a v klasickej všeobecnej relativite sa mu nedá vyhnúť. Problém nie je v tom, že by hmotnosť čiernej diery bola príliš veľká a gravitačné pole príliš silné. Keby to tak bolo, iste by šlo zostrojiť dostatočne silný raketový motor, ktorý by dokázal gravitácii vzdorovať. Problém je, že v istej vzdialenosti od čiernej diery je gravitačné pole priamo nekonečne veľké, a to aj keď je hmotnosť čiernej diery konečná.

Majme teda čiernu dieru s hmotnosťou m. Vo veľkých vzdialenostiach od čiernej diery je jej gravitačné pole úplne rovnaké, ako gravitačné pole obyčajného objektu s tou istou hmotnosťou. Ak ste dosť ďaleko od čiernej diery, podľa gravitačného poľa nepoznáte, že je to čierna diera. Indíciou, že sa o čiernu dieru jedná, by mohlo byť, že by ste nevideli objekt, ktorý vás priťahuje. Ale to by mohla byť kľudne nejaká málo jasná hviezda alebo proste obrovský kus kameňa, ktorý sám žiadne svetlo nevyžaruje.

Keď sa budete približovať k čiernej diere, gravitačné pole bude vzrastať, tak ako v prípade každého iného objektu. Stále sa však môžete vrátiť, hoci na to budete potrebovať väčší výkon motorov a budete si od kamaráta musieť na vašu raketu požičať viac benzínu. Keď však prekročíte určitú vzdialenosť smerom k čiernej diere, zistíte, že už sa vrátiť nemôžete, aj keby vaša raketa mala sebesilnejšie motory. Táto vzdialenosť sa nazýva Schwarzschildov polomer a označíme ho r_S. Čierna diera samotná je skoncentrovaná do jediného bodu, ale tento bod je obklopený myslenou guľovou plochou polomeru r_S, ktorú nazývame horizont udalostí.

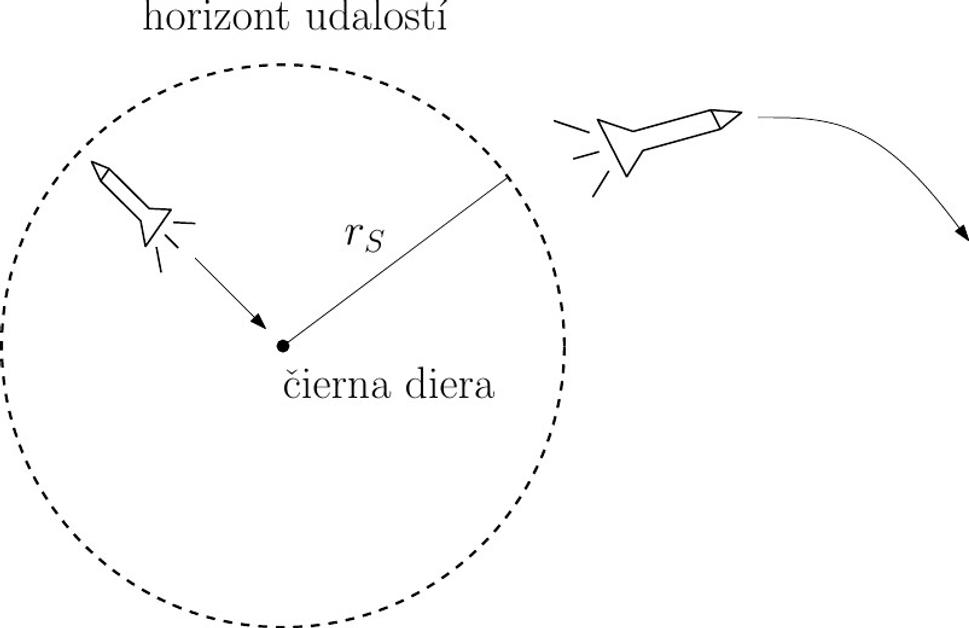
Na tomto obrázku som umelecky stvárnil čiernu dieru. Čierna diera je vlastne jediný bod v strede, kde je skoncentrovaná celá hmotnosť čiernej diery. Tento stred je ale obklopený sférou Schwarzschildovho polomeru r_S, ktorú nazývame horizont udalostí. Raketa, ktorá sa nachádza nad horizontom, si môže veselo odplávať kam chce, ale raketa pod horizontom sa navzdory ľubovoľne výkonným motorom nevyhnutne rúti do stredu čiernej diery.

Inak je zaujímavé, že podobný efekt sa realizuje aj v ekonomickej sfére. Pád do čiernej diery bol v minulosti v slovenských pomeroch realizovaný o.i. nebankovým subjektom Horizont Slovakia. Podobnosť s horizontom udalostí je zrejmá.

Toto je zjednodušený, ale celkom korektný kvalitatívny popis toho, čo sa podľa všeobecnej relativity deje v okolí Schwarzschildovej čiernej diery. Verím, že zatiaľ som o čiernych dierach čitateľovi nepovedal nič nové. Ale poďme sa pozrieť, ako to súvisí so všetkým, čo sme si povedali doteraz o priestoročasových intervaloch a kauzálnej štruktúre. Zase použijem nejaké matematické rovnice a hlavne nevysvetlím, odkiaľ sa vzali. To by bolo na niekoľko ďalších blogov. K niektorým veciam sa ešte vrátime, k iným asi nie. Ale s tým, čo sme si doteraz povedali, síce nepochopíte, prečo vyzerá Schwarzschildovo riešenie tak, ako vyzerá, ale mali by ste dokázať sledovať môj výklad a pochopiť, prečo zo Schwarzschildovho riešenia plynú exotické vlastnosti čiernych dier. To platí pre laikov, samozrejme, odborníci už dávno vedia, k čomu smerujem (smerom k ľuďom). Alebo, slovami prezidenta hlavy štátu našej krajiny, odborníci vedia, "kam sledujem".

Schwarzschildova metrika

V srdci všeobecnej relativity je zabudovaný fakt, že na popis geometrie a na popis udalostí môžeme použiť ľubovoľné súradnice. V plochom priestore sme s výhodou používali obyčajné kartézske súradnice x,y, z a časovú súradnicu t. V zakrivených priestoroch však tieto súradnice nie je možné použiť. Každý zakrivený priestor však môžeme popisovať nekonečne mnoho rôznymi súradnicovými systémami. Hovoril som, že Schwarzschildovo riešenie popisuje pole okolo telesa guľového tvaru, hovoríme, že popisuje pole so sférickou symetriou. V takýchto prípadoch je vhodné použiť tzv. sférické súradnice. Mnohí ich určite poznáte aj z elementárnejších situácií, ale nebudem tieto súradnice presne definovať. Poviem len, že v týchto súradniciach sa poloha popisuje vzdialenosťou r od stredu, a dvoma uhlami. Tie uhly nás nebudú zaujímať, ale predstavte si, že celý priestor rozvrstvíme na guľové plochy rôznych polomerov, ako na tomto obrázku (pozor, nie je to priestoročasový diagram, je to obyčajný priestor)

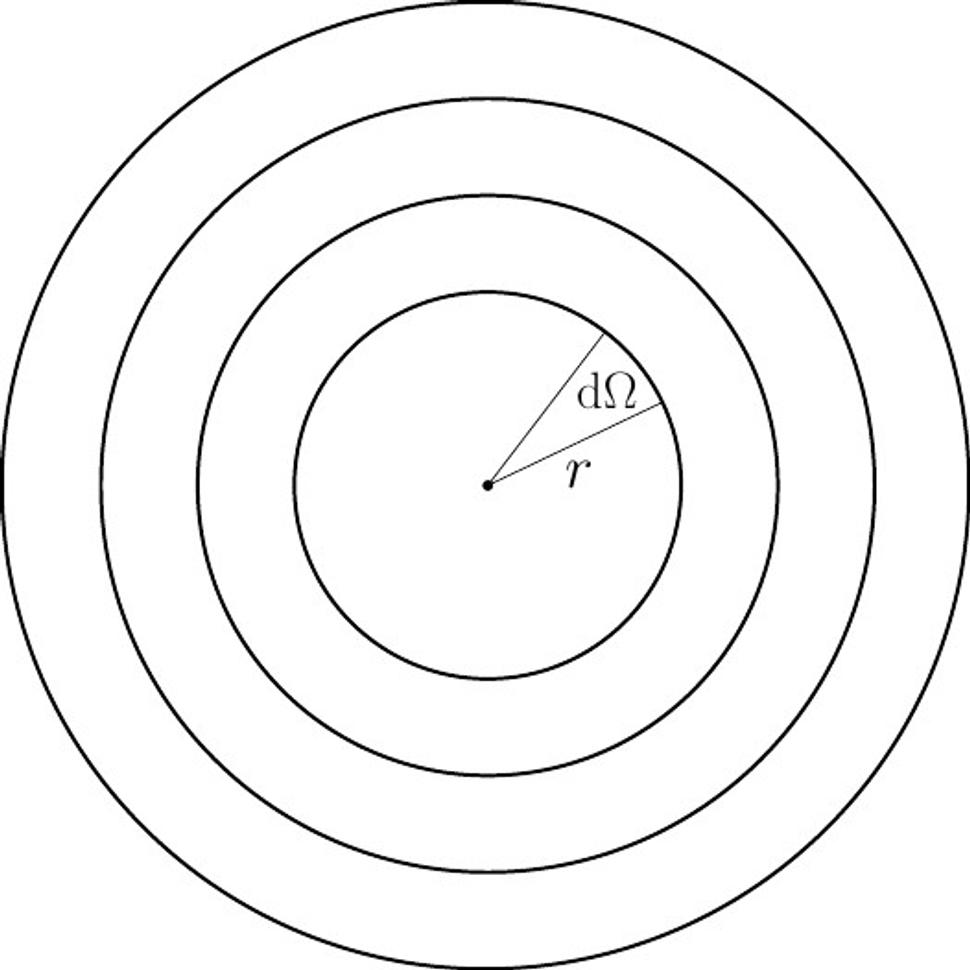
Na tomto obrázku je r polomer guľovej plochy, teda vzdialenosť od stredu, a dΩ je priestorový uhol. Obrázok je dvojrozmerný, ale určite si viete predstaviť, že priestorový uhol na každej guľovej ploche vytína maličkú plôšku.

No a Schwarzschild ukázal, že v okolí čiernej diery nemá metrika priestoročasu tvar

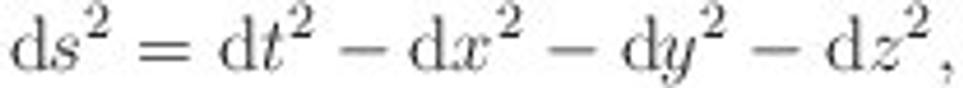
ako v Minkowského priestore. Metrika okolo čiernej diery (nerotujúcej) je

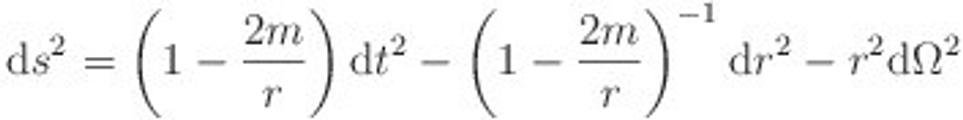
Konštanta m je hmotnosť čiernej diery, r je sférická súradnica a dΩ je priestorový uhol. Nepovieme si teda, prečo má metrika práve tento tvar, ale berme ako fakt, že je to riešenie Einsteinových rovníc. A vidíme, že je pomerne jednoduché. Pretože vlastnosti gravitačného poľa v tomto prípade (guľová symetria!) nezávisí na smere, nebudeme si všímať časť s priestorovým uhlom, a budeme uvažovať len metriku v tvare

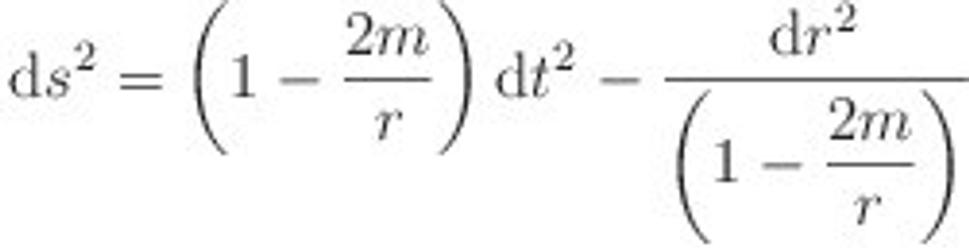
Na prvý pohľad vidíme z tejto metriky dve veci. Prvá: ak budeme vo veľkej vzdialenosti od čiernej diery, teda keď r bude veľmi veľké číslo, tak zlomok 2 m/r bude naopak veľmi malé číslo, ktoré môžeme voči jednotke zanedbať. Metrika sa vtedy zredukuje na

,

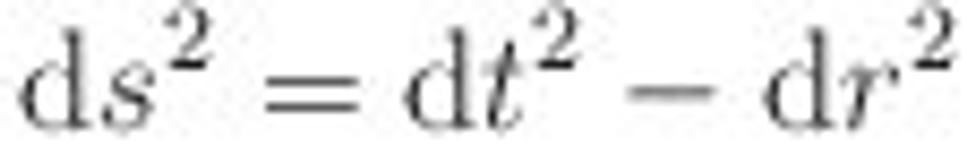
presne ako v Minkowského priestoročase. To znamená, že vo veľkej vzdialenosti od čiernej diery je krivosť priestoru nulová, takže gravitačné pole ďaleko od čiernej diery slabne a klesá k nule. Takéto priestoročasy sa nazývajú asymptoticky ploché, teda ploché vo veľkej vzdialenosti od zdroja. Podobne ak položíme m = 0, dostaneme znovu Minkowského metriku. Takže ak má čierna diera nulovú hmotnosť, jej gravitačné pole je nulové. Takže Schwarzschildova metrika v limitných prípadoch dáva rozumné výsledky.

Druhá vec, ktorú si všimneme, spočíva v tomto. Vieme, že deliť nulou sa nedá (hoci na blogu sme.sk v sekcii "veda" som videl aj zástancov opačného názoru :) ). Keď sa snažíme deliť nulou, môžeme to chápať ako limitný proces, kedy delíme stále menším a menším číslom. Výsledok takého delenia je naopak stále väčšie číslo, takže väčšinou platí, že delenie nulou znamená nekonečne veľký výsledok.

V Schwarzschildovej metrike sa môže deliť nulou hneď dvakrát. Jednak vo výraze 2 m / r, ktorý je pre r = 0 nekonečný. Ale okrem toho môže byť nulový menovateľ v člene dr². Ak bude platiť

r = 2 m,

potom menovateľ v člene s dr² bude nulový a teda tento člen bude nekonečný.

V relativite takýmto prípadom hovoríme singularity. Schwarzschildova metrika má dve singularity:

- prvá, keď r = 0. Táto singularita sa nazýva krivostná singularita, pretože krivosť priestoročasu je v tomto bode nekonečná. Keď sa hovorí o singularitách čiernych dier, myslí sa práve táto krivostná singularita. Objekt, ktorý do nej spadne, prestáva existovať a jeho hmotnosť prispeje k celkovej hmotnosti čiernej diery.

- druhá, keď r = 2 m. Táto singularita sa nazýva súradnicová, a to z dôvodov, ktoré teraz nebudem rozoberať, ale budú dôležité neskôr.

Ale všimnite si, že už zo samotnej Schwarzschildovej metriky je vidieť, že v okolí r = 2 m sa bude diať niečo zvláštne. Táto hodnota polomeru je práve Schwarzschildov polomer r_S, o ktorom sme hovorili, že predstavuje polomer horizontu udalostí! Našli sme teda vzťah pre polomer horizontu udalostí. Ak m je hmotnosť čiernej diery, potom Schwarzschildov polomer horizontu udalostí je

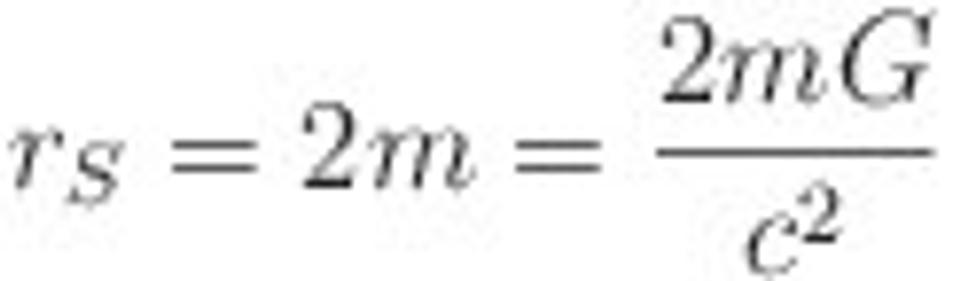
V druhej rovnosti som použil obvyklé jednotky, teda jednotky v ktorých je rýchlost svetla c=300 000 km/s, a nie c=1. Veličina G je gravitačná konštanta. Ukázal som tento vzťah s obvyklými jednotkami, keby ste chceli mať predstavu o veľkosti Schwarzschildovho polomeru pre reálne telesá. Napríklad pre čiernu dieru hmotnosti Slnka vyjde polomer horizontu udalostí necelé 3 kilometre. Takže Slnko by muselo byť nahňahňané v oblastimeru 3km, aby sa z neho stala čierna diera. Pre Zem táto hodnota vychádza na asi 9 mm. V ďalšom sa však vrátime k pohodlnejším jednotkám a za Schwarzschildov polomer budeme považovať veličinu r_S=2 m.

Tak a poďme do finále!

Kauzálna štruktúra Schwarzschildovej geometrie

Videli sme, že vo vzdialenosti r_S od stredu čiernej diery sa deje niečo zvláštne, pretože metrika je v tejto vzdialenosti singulárna. Prezradil som, že táto vzdialenosť zodpovedá horizontu udalostí, ale poďme sa detailne pozrieť na to, prečo raketa nad horizontom môže odletieť, ale spod horizontu už nie.

Vieme už, že každý objekt sa môže pohybovať len vo vnútri svetelného kužeľa. Vyšetrime teda, ako vyzerajú svetelné kužele v okolí čiernej diery. Zistili sme, že vo veľkej vzdialenosti od čiernej diery je priestor plochý, takže tam budú svetelné kužele vyzerať rovnako, ako v Minkowského priestoročase. Inými slovami, svetlo sa v priestoročasovom diagrame šíri pod uhlom 45 stupňov a všetky podsvetelné objekty sa musia pohybovať vnútri tohto kužeľa.

Ako sa situácia zmení, keď sa priblížime k čiernej diere? Predpokladajme, že sme už blízko čiernej diery, ale stále nad horizontom, teda r > r_S. Ako zistíme tvar svetelného kužeľa? Na začiatku sme vysvetlili, že priestoročasový interval je pre svetelný signál vždy nulový, musí teda platiť

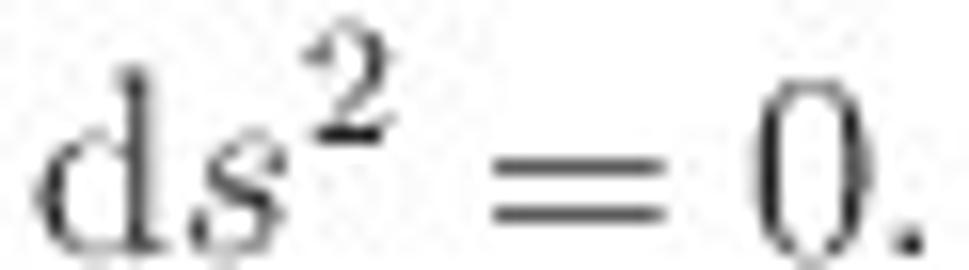
Ak za ds dosadíme zo vzťahu pre Schwarzschildovu metriku, dostaneme podmienku

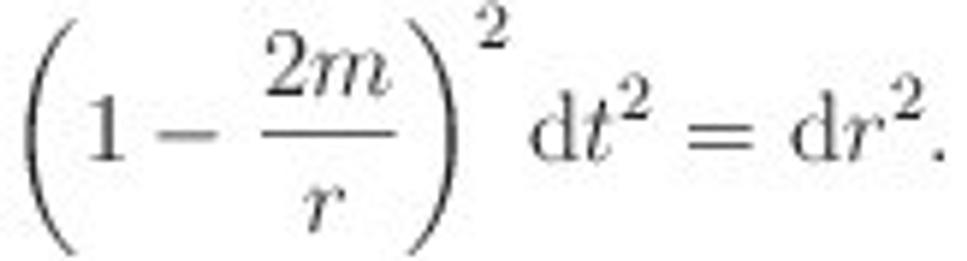
Po odmocnení máme

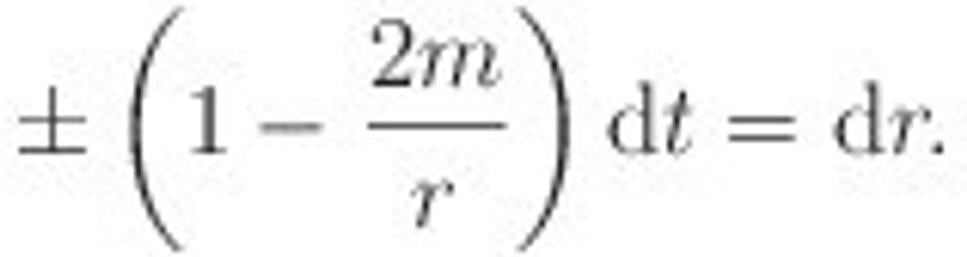
Znamienka + a - reprezentujú budúci a minulý svetelný kužeľ. Čo vlastne hovorí posledná rovnica? Pre jednoduchosť zvoľme len znamienko +. Hovorí, že ak sa v smere časovej osi pohneme o malý úsek dt, musíme sa v smere osi r posunúť o úsek (1-2m/r) dt. Je to úsek väčší, či menší? Pretože sme nad horizontom, r > r_S = 2 m, zlomok 2 m / r je menší než jedna, takže celá zátvorka je kladná, ale menšia, než jedna. Z toho plynie, že v smere osi r sa musíme posunúť o menší úsek, než v smere osi t. To vedie k tomu, že svetelné kužele sa zužujú, naťahujú vo vertikálnom smere. Čím bližšie horizontu udalostí sme, tým sú kužele užšie a užšie. Priamo na horizonte majú nulovú šírku.

Ale na horizonte sa stane to, že sa kužele preklopia. Skutočne, ak predpokladáme, že r < r_S = 2m, celá zátvorka sa stane zápornou, takže os svetelného kužeľa už nebude zvislá, ale vodorovná. Pokúsil som sa to znázorniť na nasledujúcom, nie príliš vydarenom obrázku:

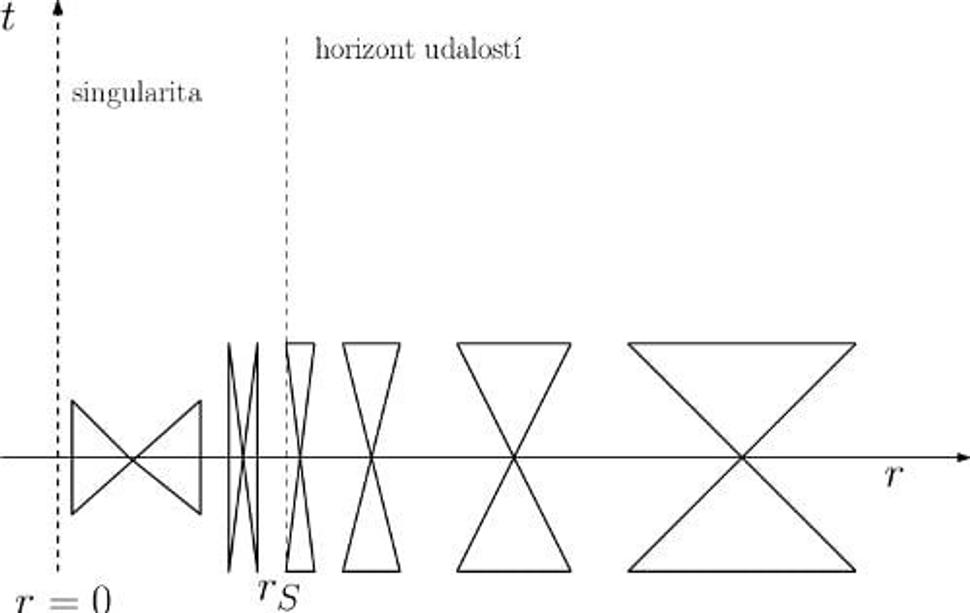
Na tomto obrázku, akokoľvek je škaredý (časom skúsim vyrobiť nejaký krajší), vidíme osi t a r. Kužeľ úplne vpravo reprezentuje svetelný kužeľ vo veľkej vzdialenosti od čiernej diery. Povedali sme, že takýto kužeľ sa zhoduje s kužeľom v plochom priestore, teda svetlo sa šíri pod uhlom 45 stupňov. Ako sa približujeme k horizontu udalostí, na obrázku je to zvislá čiarkovaná čiara na polomeri r_S, kužele sa zužujú. Za horizontom sa preklopia, takže ukazujú smerom k singularite, k stredu čiernej diery v r = 0.

Ale spomeňme si ešte raz, že reálny pozorovateľ sa môže vždy pohybovať len vnútri svetelného kužeľa. Na pravo od Schwarzschildovho polomeru ukazujú kužele smerom nahor, takže pozorovateľ sa môže vzďaľovať od čiernej diery. Keď sa ale kužele za horizontom preklopia, nemá na výber a nutne musí skončiť v singularite.

Takto sme názorne nakreslili situáciu v okolí čiernej diery. Dúfam, že sa mi podarilo hlavné myšlienky zrozumiteľne vysvetliť. Síce som nepovedal, kde sa vzala Schwarzschildova metrika, jej dôsledky sú snáď pochopiteľné. Videli sme, že táto metrika skutočne popisuje čiernu dieru, teda objekt, ktorý má horizont udalostí, spod ktorého už niet úniku. A snáď som na vás preniesol aspoň trochu pocitu krásy z Einsteinovej teórie, ktorá dokáže geometrickým jazykom popísať gravitáciu a rôzne exotické vlastnosti tejto prapodivnoúchvatnej sily. Pri štúdiu tejto teórie som bol vždy nadšený z toho, ako elegantne to všetko funguje. Či už ste nábožensky založený a máte birmovku, alebo ste pravoverný ateista (alebo oboje), pri štúdiu týchto vecí sa vás musí zmocniť pocit, že skutočne vidíte niečo podstatné z prírodných zákonov.

Nabudúce budeme pokračovať (ešte si rozmyslím, o čom presne), ale čakajú nás ešte zaujímavejšie veci: nabité a rotujúce čierne diery s dvoma horizontmi, popis kolapsu hmotných hviezd, teorémy o singularitách, Penroseove diagramy etc.